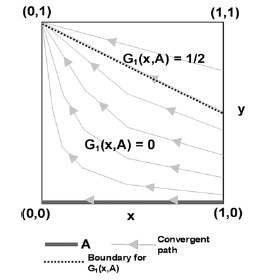
This paper studies stochastic stability methods applied to processes on general state spaces. This includes settings in which agents repeatedly interact and choose from an uncountable set of strategies. Dynamics exist for which the stochastically stable states differ from those of any reasonable finite discretization. When there are a finite number of rest points of the unperturbed dynamic, sufficient conditions for analogues of results from the finite state space literature are derived and studied. Illustrative examples are given.
Published in the Journal of Mathematical Economics (2015). Link to paper.